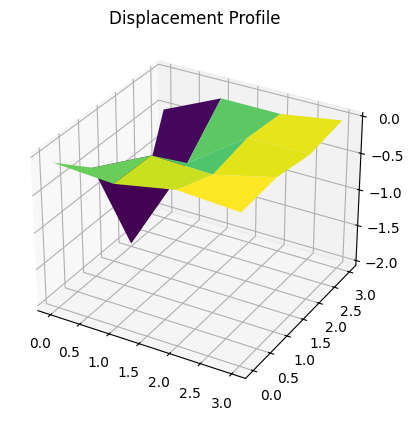
Quanta utilizes finite element analysis (FEA) and quantum computing to simulate the behavior of nanomaterials under pressure, enabling groundbreaking advancements in engineering and science.

THE QUANTUM ADVANTAGE.
Asymptotic Advantage
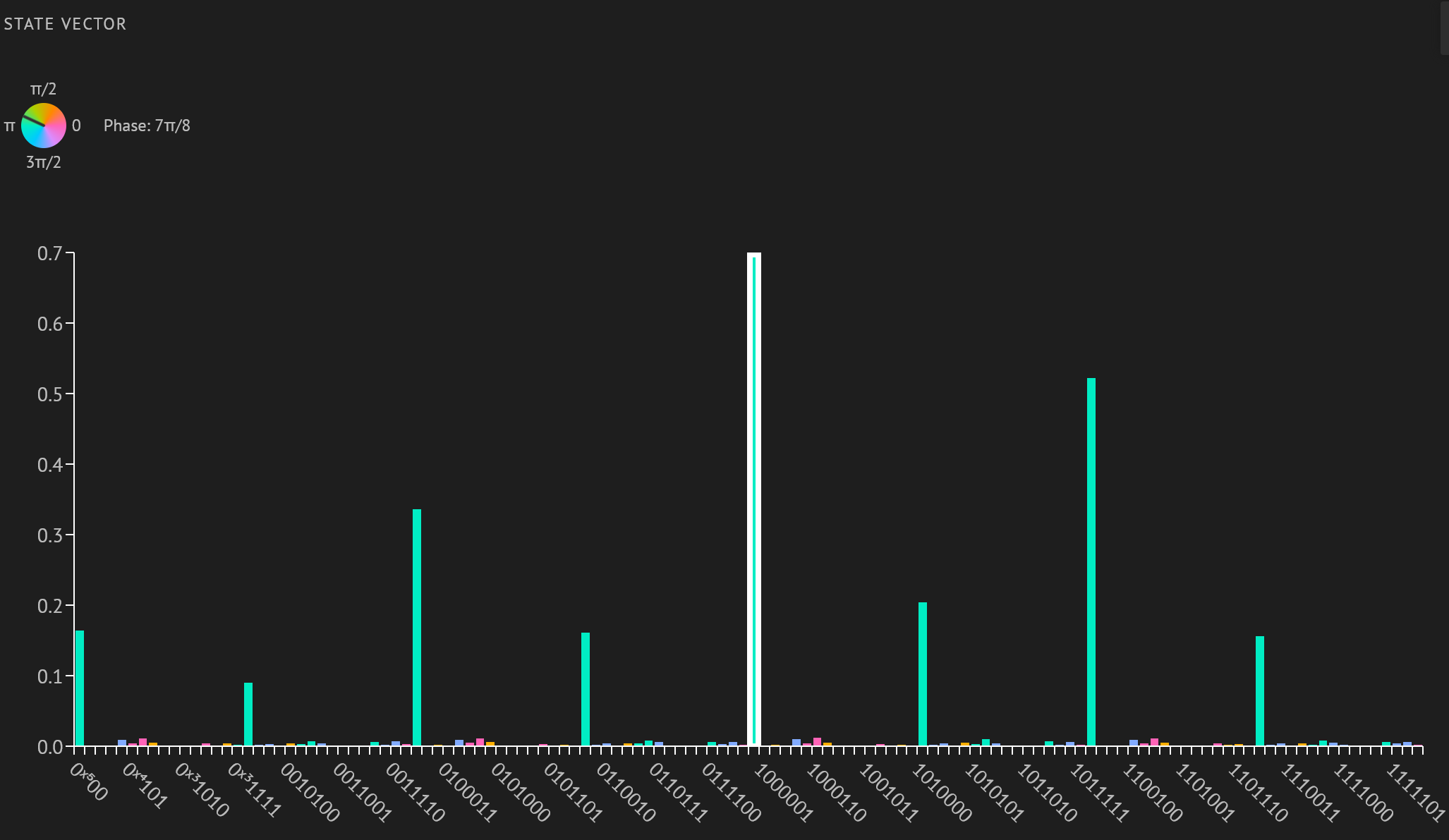
The HHL algorithm is used to solve the system of linear equations to determine displacement. The HHL algorithm is a quantum algorithm that solves linear systems of equations in O(log(N)k2) time, exponentially faster than classical, which can run in O(Nk) at best.
Accuracy
Our quantum solution has 98%+ fidelity to classical.
Scalability
The HHL algorithm can be easily implemented with the Suzuki-Trotter decomposition to increase scalability.

Quantum computation is the future. Don't let classical hold you back.
Use Quanta to put yourself at the forefront of computing and engineering.
QUANTUM-ASSISTED NANO-STRUCTURAL ANALYSIS
Quanta uses finite element analysis to model the behavior of nanomaterials under force as differential equations. The differential equations are minimized into a system of linear equations, and then solved using the HHL algorithm on a quantum computer. The displacement is collected and graphed, and results are then used to predict how nanomaterials will react under force, and to optimize their design for specific applications.
Step 1
Give Quanta details on what you want to model.
Step 2
Quanta pulls real data on the material.
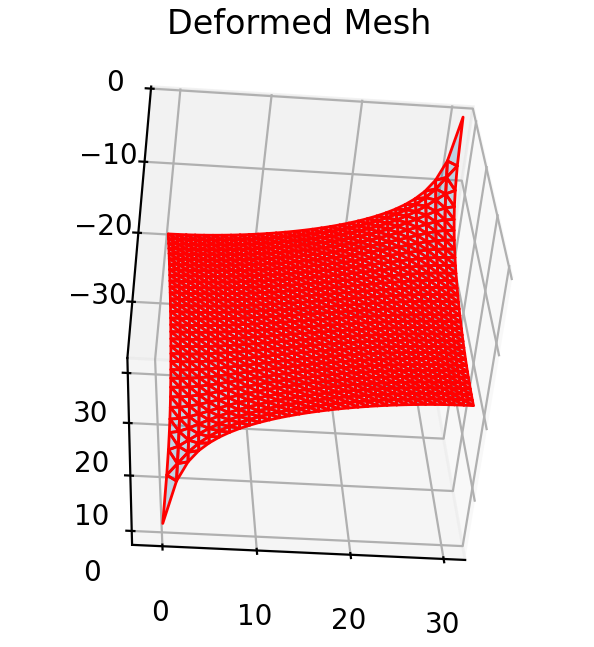
Step 3
The material is represented as a mesh, and finite element analysis is run on it to simulate force.
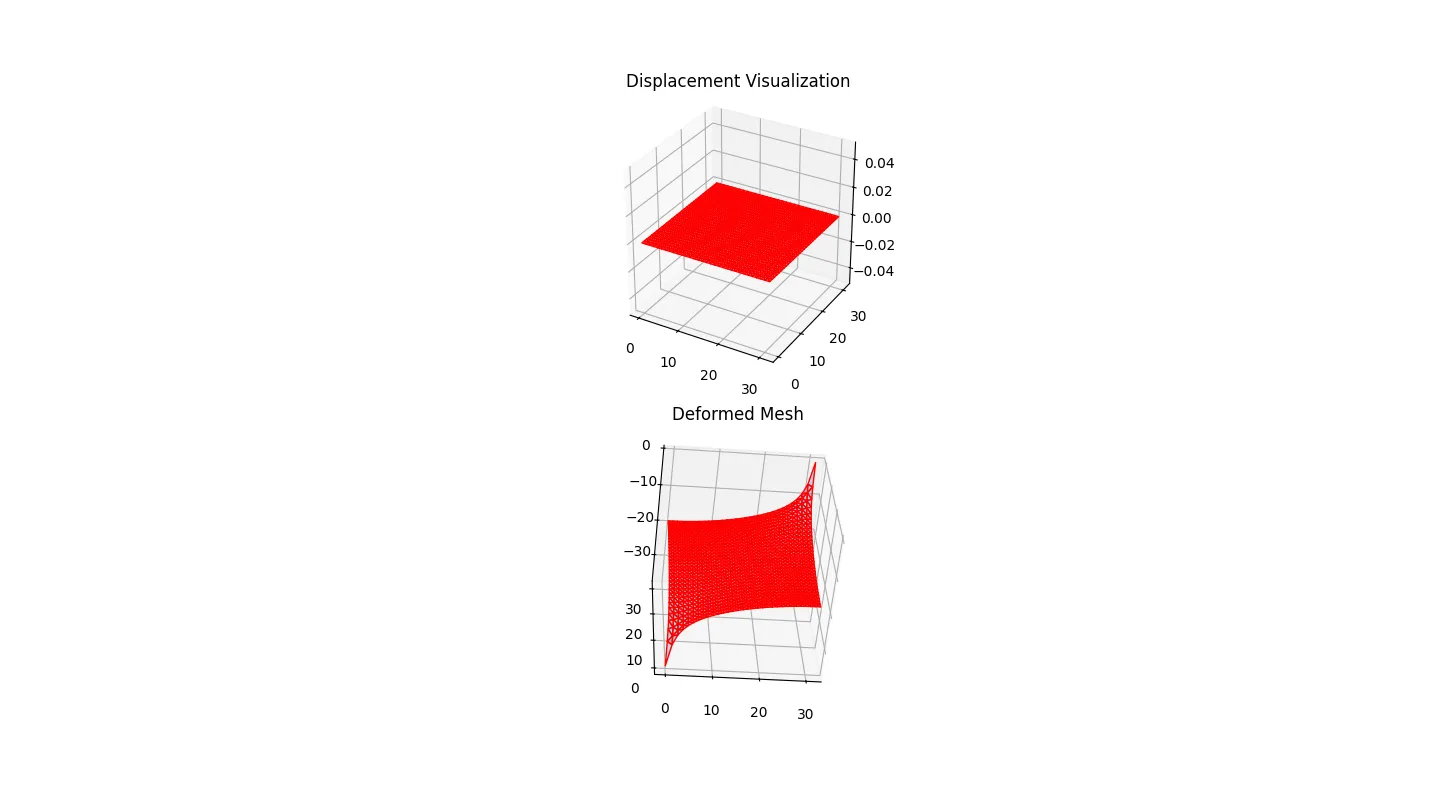
Step 4
Voila! See your model and how it warps under stress. Use this to know how much force your material can take, and how to optimize it for your needs.